snd-wav.htm
by U Kyaw Tun (UKT) (M.S., I.P.S.T., USA) and staff of Tun Institute of Learning (TIL) . Not for sale. No copyright. Free for everyone. Prepared for students and staff of TIL Research Station, Yangon, MYANMAR : http://www.tuninst.net , www.romabama.blogspot.com
UKT: This whole chapter is on Physics, no mathematics and a lot of animations to explain the ideas involved.
01. How is sound produced?
02. Transverse waves and longitudinal waves
03. Sound waves -- listen to
<)) 300 Hz
04. Standing wave and traveling wave
05. Superposition of sine waves
06. Fourier Analysis and Synthesis
07. Time domain vs. Frequency domain: Fourier transform
Passages worthy of note:
UKT notes
• loudness and intensity
• pitch and frequency
This chapter is about sound waves, and you might say, "
Why should we be bothered with sound waves? We are speaking
about Burmese-Myanmar language, aren't we?" Yes, we are.
But we will get bogged down when we describe consonants in phonetic terms
according to where they take place (POA or Point of articulation), how
they are articulated (‘manner’) and whether the vocal folds are vibrating
(‘voicing’). This three-way description of consonants is often known as the
VPM (voice-place-manner) description, and it can be used to describe
consonants in any human language. There are other features of articulation
that may also be relevant in particular cases (for example aspiration --
which is looked upon differently in Burmese-Myanmar as
{ha.hto:} formation), but in general, the VPM description is sufficient
to characterise the different consonants of a language.
We will come into more misunderstandings
when we look into the pronunciation of vowels. There are
two languages involved in our discussion: Burmese-Myanmar
and English-Latin. Then we will have to include Hindi-Devanagari because of our
interest in comparing Pali-Myanmar to Pali-Latin and Pali-Devanagari. Burmese,
English and Hindi are living languages and all are
changing across time, and across geographical space.
We became confused with written scripts -- the abugida
and the alphabet -- and we forget that they are meant
to "record" human speech. We tend to say
"That was the Pali sound in old days"
or "the ancient pronunciations", forgetting that
none of us have ever heard with our own ears what we are talking about.
We forget that the machines to record the sounds and pronunciations
have not been invented until recently. We forget that
the Burmese-Myanmar word for 'Grammar' came from the Pali-Myanmar word
{žūd~da.} meaning "sound". So, unless we start
from sound, there would never be an end to our mis-interpretations
and mis-understandings. But then, people like my good friend U Tun Tint
of the MLC would say something like, "The positions of the places in the mouth where
these sounds are produced are so definitely describe that we know what Pali
sounds are like." That is the position of many linguists and phoneticians who
have not realized that where the vowels are produced. The vowels are produced deep down in the throat
where direct observation has not been possible up to about 40 years ago. Even
then, much of our knowledge has come from the field of surgery of the larynx and
its rehabilitation. The results of the recent research, described under the
umbrella term 'Voice Quality' (VQ), is being continually applied to computer
voice recognition and voice production systems.
Though this chapter is based on mostly on the work of Kevin Russell, University of Manitoba, which I have downloaded more than 5 years ago, and which has been accessed quite often, I have included materials from many other sources, such as Lesley Jeffries' Discovering Language: The Structure of Modern English, Palgrave Macmillan, 2006, etc.
Since sound (or specifically sound energy) travels in waves, let's start with waves.
From HyperPhysics http://hyperphysics.phy-astr.gsu.edu/hbase/sound/tralon.html 080330
For
transverse waves the displacement of the medium is perpendicular to the
direction of propagation of the wave. A ripple on a pond and a wave on a string
are easily visualized transverse waves.
Transverse waves cannot propagate in a gas or a liquid because there is no mechanism for driving motion perpendicular to the propagation of the wave.
In longitudinal waves the displacement of the medium is parallel to the propagation of the wave. A wave in a "slinky" is a good visualization. Sound waves in air are longitudinal waves.
Sound energy is transmitted through air as the medium.
Of course, sound can be transmitted across water, and
even across metal wire and cotton thread as every
school boy of my age knows.
I am thinking about two tin cans with a stretched string
in between which we used as "telephone".
Here, we are talking about sound being transmitted through
air which becomes rarified and compressed as the sound energy
is being carried across.
The simplest laboratory instrument we can use to produce sound is the tuning fork. The pix on the right, Fig.5.02, shows the rarefaction and compression pockets of air molecules as sound produced by a tuning fork is carried across. The following animation from http://www.glenbrook.k12.il.us/GBSSCI/PHYS/mmedia/waves/harm4.html.
 Remember, the air molecules do not travel. It is the
"pattern" that is traveling.
Remember, the air molecules do not travel. It is the
"pattern" that is traveling.
Rarefaction and compression sections (produced in a 'slinky"
travelling from left to right in what is known as a longitudinal wave.
Sound waves are longitudinal waves.
For mathematical analysis, we use another figure or graph, Fig.5.03. The rarefaction and compression pattern quantified by air-pressure is shown by the Y-axis, and time by the X-axis. This simplest kind of pressure wave is called a sine wave.
Two important properties of a sine wave that can be measured are:
1. amplitude (or sometimes erroneously called loudness, size of pressure differences) usually measured in decibels (dB) , and
2. frequency (or sometimes erroneously called pitch) usually measured in cycles per second, or Hertz (Hz) (Note: wavelength is the "reciprocal" of frequency, and is not usually given. Sound is generally described in terms of frequency and not wave length. Since, there is definite relationship between two, we can always find out the wave length from frequency, remembering that In a particular medium (such as as air), all sound waves travel at the same "speed" or velocity which is about 330 meters per second:
.
The word 'pitch' must always be used with caution. It is a perceived quality, whereas the frequency is a measurable quantity. Because pitch is a confusing term, it will be described in a separate section below.
Fig. 5.03. is for a particular sound with a particular quality.
If you were to change either the amplitude or the time,
you will get other sounds with other qualities. See figures Sine waves
compared a and b.
When we say "sound being carried across the air medium", what we are actually talking about is a form of energy (call it sound energy) being transmitted across space. Because, sound is energy, various sound waves can be combined to produce other sounds with other qualities. The result is the simple sine waves becoming more complex. In Fig.5.05, we are showing the result of adding waves 1 and 2 (red) to produce a resultant wave (blue). Adding sound waves is easy. But given the blue resultant wave, can we split it up into the original red waves? It is not easy and it calls for a "complex" mathematical treatment.
First, let's listen to various sound waves from Kevin Russell's website, from which I have downloaded the following on 071221. Click on the sound buttons given.
They can be added (superimposed) together:

to produce a complex wave:
<)) 300Hz + 500Hz
This is important because: Any complex wave can be treated as a combination of simple sine waves.
We usually don't care about the actual complex wave itself. We're only interested in the frequencies and amplitudes of the simple waves that it's made of. Two more examples:
<))
300 Hz and 2000 Hz added (fake [ i ])
<))
900 Hz and 1100 Hz added (fake [ a ])
From: HyperPhysics
http://hyperphysics.phy-astr.gsu.edu/Hbase/waves/standw.html 080331
Waves produced in a string tied at both ends will travel back and forth between the ends producing what is known as a standing wave. A standing wave can also occur in an column of air closed at both ends. However, if only one end of the string is tied, or if the column of air is closed only at one end, the wave produced is a traveling wave.
An ideal vibrating string will vibrate with its fundamental frequency
and all harmonics of that frequency. The position of nodes and antinodes
is just the opposite of those for an open air column.
In both types of vibration, the lowest
resonant frequency of a vibrating object is called its fundamental
frequency. Most vibrating objects have more than one resonant frequency and
those used in musical instruments typically vibrate at harmonics of the
fundamental. A harmonic is defined as an integer (whole number) multiple of the
fundamental frequency. Vibrating
strings,
open cylindrical air columns, and
conical air columns will vibrate at all harmonics of the fundamental.
Cylinders with one end closed will vibrate with only odd harmonics
of the fundamental. Vibrating
membranes typically produce vibrations at harmonics, but also have some
resonant frequencies which are not harmonics. It is for this class
of vibrators that the term
overtone becomes useful - they are said to have some non-harmonic overtones.
In naturally occurring vibrations, there is a harmonic at each multiple of the fundamental frequency -- theoretically all the way up to infinity, though the harmonics decrease in amplitude as the frequency rises.
The following animations are from: http://www.glenbrook.k12.il.us/GBSSCI/PHYS/mmedia/waves/harm4.html. (UKT: no longer on the Internet on 130816).


The formation of the standing wave can be thought of as a wave traveling from the left end to the right end, and then reflected back to the left end.


The upper-right animation shows a red crest traveling from left end of the tied string to right end. At the right end, it is reflected becoming a blue trough, and the trough travels back to the left-end.
Remember a node is a place which remains stationary. A place showing maximum movement is an anti-node. See the three standing waves below:
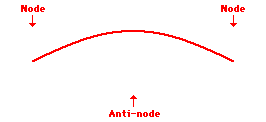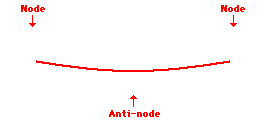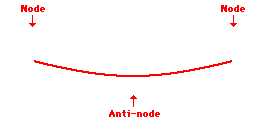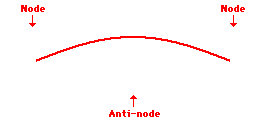 First harmonic
First harmonic
 Second harmonic
Second harmonic
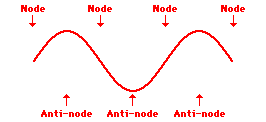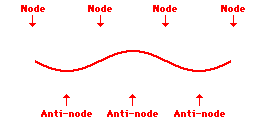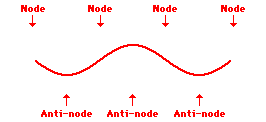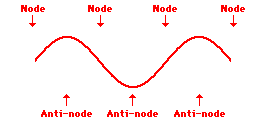 Third harmonic
Third harmonic
From: www.kettering.edu/~drussell/Demos/superposition/superposition.html 080330
 The
principle of superposition may be applied to waves whenever two (or more) waves
travelling through the same medium at the same time. The waves pass through each
other without being disturbed. The net displacement of the medium at any point
in space or time, is simply the sum of the individual wave dispacements. This is
true of waves which are finite in length (wave pulses) or which are continuous
sine waves. Now, let's look at some animations of superposition of two waves.
The
principle of superposition may be applied to waves whenever two (or more) waves
travelling through the same medium at the same time. The waves pass through each
other without being disturbed. The net displacement of the medium at any point
in space or time, is simply the sum of the individual wave dispacements. This is
true of waves which are finite in length (wave pulses) or which are continuous
sine waves. Now, let's look at some animations of superposition of two waves.
The movie at right shows two gaussian wave pulses are travelling on a string, one is moving to the right, the other is moving to the left. They pass through each other without being disturbed, and the net displacement is the sum of the two individual displacements. It should also be mentioned that this string is nondispersive (all frequencies travel at the same speed) since the Gaussian wave pulses do not change their shape as they propagate. If the medium was dispersive, then the waves would change their shape.
 Two waves (with the same amplitude, frequency, and wavelength) are travelling in the
same direction on a string. Using the principle of superposition, the resulting
string displacement may be written as:
Two waves (with the same amplitude, frequency, and wavelength) are travelling in the
same direction on a string. Using the principle of superposition, the resulting
string displacement may be written as:
where:
y = amplitude (in terms of x, and t)
ym = maximum amplitude
ϕ (letter phi) = phase difference
ѡ (letter omega) = angular velocity of the frequency vector
t = time
which is a travelling wave whose amplitude depends on the phase (phi). When the two waves are in-phase (phi=0), they interfere constructively and the result has twice the amplitude of the individual waves. When the two waves have opposite-phase (phi=180), they interfere destructively and cancel each other out.
The animation at right shows two sinusoidal waves travelling in the same direction. The phase difference between the two waves varies increases with time so that the effects of both constructive and destructive interference may be seen. First of all, notice that the sum wave (in blue) is a travelling wave which moves from left to right. When the two gray waves are in phase the result is large amplitude. When the two gray waves become out of phase the sum wave is zero.
 A
travelling wave moves from one place to another, whereas a standing
wave appears to stand still, vibrating in place. Two waves (with the same
amplitude, frequency, and wavelength) are travelling in opposite directions on a
string. Using the principle of superposition, the resulting string displacement
may be written as:
A
travelling wave moves from one place to another, whereas a standing
wave appears to stand still, vibrating in place. Two waves (with the same
amplitude, frequency, and wavelength) are travelling in opposite directions on a
string. Using the principle of superposition, the resulting string displacement
may be written as:
This wave is no longer a travelling wave because the position and time dependence have been separated. The displacement of the string as a function of position has an amplitude of 2ymsin kx. This amplitude does not travel along the string, but stands still and oscillates up and down according to cos wt. Characteristic of standing waves are locations with maximum displacement (antinodes) and locations with zero displacement (nodes).
The movie at right shows how a standing wave may be created from two travelling waves. If two sinusoidal waves having the same frequency (wavelength) and the same amplitude are travelling in opposite directions in the same medium then, using superposition, the net displacement of the medium is the sum of the two waves. As the movie shows, when the two waves are 180° out-of-phase with each other they cancel, and when they are in-phase with each other they add together. As the two waves pass through each other, the net result alternates between zero and some maximum amplitude. However, this pattern simply oscillates; it does not travel to the right or the left. I have placed two dots on the string, one at an antinode and one at a node. Which is which?
 Two
waves of equal amplitude are travelling in the same direction. The two waves
have different frequencies and wavelengths, but they both travel with the same
wave speed. Using the principle of superposition, the resulting particle
displacement may be written as:
Two
waves of equal amplitude are travelling in the same direction. The two waves
have different frequencies and wavelengths, but they both travel with the same
wave speed. Using the principle of superposition, the resulting particle
displacement may be written as:
This resulting particle motion is the product of two travelling waves. One part is a sine wave which oscillates with the average frequency f = ½(f1 + f2). This is the frequency which is perceived by a listener. The other part is a cosine wave which oscillates with the difference frequency f = ½(f1 - f2). This term controls the amplitude "envelope" of the wave and causes the perception of "beats". The beat frequency is actually twice the difference frequency, fbeat = (f1 - f2).
In the movie at left two waves with slightly different frequencies are travelling to the right. The resulting wave travels in the same direction and with the same speed as the two component waves. The "beat" wave oscillates with the average frequency, and its amplitude envelope varies according to the difference frequency.
From: http://hyperphysics.phy-astr.gsu.edu/Hbase/audio/Fourier.html#c1 080330
The mathematician Fourier proved that any continuous function could be produced as an infinite sum of sine and cosine waves. His result has far-reaching implications for the reproduction and synthesis of sound. A pure sine wave can be converted into sound by a loudspeaker and will be perceived to be a steady, pure tone of a single pitch. The sounds from orchestral instruments usually consists of a fundamental and a complement of harmonics, which can be considered to be a superposition of sine waves of a fundamental frequency f and integer multiples of that frequency.
The process of decomposing a musical instrument sound or any other periodic function into its constituent sine or cosine waves is called Fourier analysis. You can characterize the sound wave in terms of the amplitudes of the constituent sine waves which make it up. This set of numbers tells you the harmonic content of the sound and is sometimes referred to as the harmonic spectrum of the sound. The harmonic content is the most important determiner of the quality or timbre of a sustained musical note.
Once you know the harmonic content of a sustained musical sound from Fourier analysis, you have the capability of synthesizing that sound from a series of pure tone generators by properly adjusting their amplitudes and phases and adding them together. This is called Fourier synthesis.
One of the important ideas for sound reproduction which arises from Fourier analysis is that it takes a high quality audio reproduction system to reproduce percussive sounds or sounds with fast transients. The sustained sound of a trombone can be reproduced with a limited range of frequencies because most of the sound energy is in the first few harmonics of the fundamental pitch. But if you are going to synthesize the sharp attack of a cymbal, you need a broad range of high frequencies to produce the rapid change. You can visualize the task of adding up a bunch of sine waves to produce a sharp pulse and perhaps you can see that you need large amplitudes of waves with very short rise times (high frequencies) to produce the sharp attack of the cymbal. This insight from Fourier analysis can be generalized to say that any sound with a sharp attack, or a sharp pulse, or rapid changes in the waveform like a square wave will have a lot of high frequency content.
From: http://education.tm.agilent.com/index.cgi?CONTENT_ID=13 080330
The three-dimensional plot of frequency, amplitude and time that shows the relationship between the time and frequency domains. It does so by looking at the fundamental of a sine wave -- and up to three harmonics -- as they are formed by rotating vectors. It's another way to view the construction of a complex waveform.
From: HyperPhysics http://hyperphysics.phy-astr.gsu.edu/Hbase/hframe.html 080330
An oscilloscope is a device that views a waveform's voltage vs. time. It is the most general-purpose tool we have to gain insight into how a circuit or signal is performing. This plot simulates an oscilloscopes view. Look at the diagram from the lower left. What you see is an oscilloscopes view of the waveform (amplitude vs. time), which is really the vector sum of all of the sinusoidal components vs. time.
A spectrum analyzer is another visual analysis device. The spectrum analyzer works in the frequency domain. It displays the amplitude of the individual frequency components vs. frequency. If you choose "4 harmonics" and look at the 4 waveforms from a vantage point at the lower right of the drawing, you essentially see what a spectrum analyzer would display (amplitude vs. frequency). Depending upon the type of spectrum analyzer chosen, the phase relationships of the frequency components may or may not be preserved. Looking from the lower left, you get an oscilloscope's view of the waveform (amplitude vs. time).
UKT: The following frames are captured from the inter-active Java applet: http://education.tm.agilent.com/index.cgi?CONTENT_ID=13, 080331, showing time-domains and frequency-domains. The first 6 frames show how the curves are traced out as the fundamental frequency vector rotates in a counter-clockwise direction.
UKT: The following 4 frames show the time-domain and frequency-domain traces for up to 3 harmonics.
While the intensity of a sound is a very objective quantity which can be measured with sensitive instrumentation, the loudness of a sound is more of a subjective response which will vary with a number of factors. The same sound will not be perceived to have the same loudness to all individuals. Age is one factor which effects the human ear's response to a sound. Quite obviously, your grandparents do not hear like they used to. The same intensity sound would not be perceived to have the same loudness to them as it would to you. Furthermore, two sounds with the same intensity but different frequencies will not be perceived to have the same loudness. Because of the human ear's tendency to amplify sounds having frequencies in the range from 1000 Hz to 5000 Hz, sounds with these intensities seem louder to the human ear. Despite the distinction between intensity and loudness, it is safe to state that the more intense sounds will be perceived to be the loudest sounds.
Go back loudness-note-b
Excerpt from: Physics Classroom Tutorial, www.glenbrook.k12.il.us/gbssci/phys/Class/sound/u11l2a.html 080326
The sensation of a frequencie(s) is commonly referred to as the pitch of a sound. [UKT: Compare the effect of light frequency being sensed by the eye.] A high pitch sound corresponds to a high frequency sound wave [If color - violet] and a low pitch sound corresponds to a low frequency [If color - red] sound wave.
Amazingly, many people, especially those who have been musically trained, are capable of detecting a difference in frequency between two separate sounds which is as little as 2 Hz. When two sounds with a frequency difference of greater than 7 Hz are played simultaneously, most people are capable of detecting the presence of a complex wave pattern resulting from the interference and superposition of the two sound waves. Certain sound waves when played (and heard) simultaneously will produce a particularly pleasant sensation when heard, are are said to be consonant. [{meaning different from that used in Linguistics}}. Such sound waves form the basis of intervals in music. For example, any two sounds whose frequencies make a 2:1 ratio are said to be separated by an octave and result in a particularly pleasing sensation when heard. That is, two sound waves sound good when played together if one sound has twice the frequency of the other. Similarly two sounds with a frequency ratio of 5:4 are said to be separated by an interval of a third; such sound waves also sound good when played together.
Go back pitch-note-b
Contents of this page
End of TIL file.